〒103-0008 東京都中央区日本橋中洲2-3 サンヴェール日本橋水天宮605
受付時間 | 9:00~17:00 |
|---|
定休日 | 土曜、日曜、祝祭日 |
|---|
ケー・イプシロン(k-ε)2方程式モデルはこんなに違う 1方程式モデルとの比較
ケー・イプシロン(k-ε)2方程式モデルの解析結果は、他の方式と比べて相当計算結果が違います。まず、1方程式モデルと比較してみましょう。下の図は高さ45メートル、幅75メートル、奥行き15メートルの板状のマンションのモデルです。高さは15階建て相当です。この建物に正面から風が吹いてきた場合に、建物側方にできる風速増加域を計算してみました。風速増加域とは、建物の建設前後で比べて、風速の比が1.1以上となる範囲のことで、いわゆるビル風の範囲を表しています。
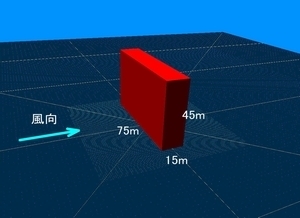
下の図は、上の図に表す建物の風速増加域を、①風洞実験、②ケー・イプシロン(k-ε)2方程式モデル、③1方程式モデルでそれぞれ求めたものです。いずれも当社が行ったものであり、平面的な風速の分布を(左右対称なので)建物の右側部分だけ表して比較しています。
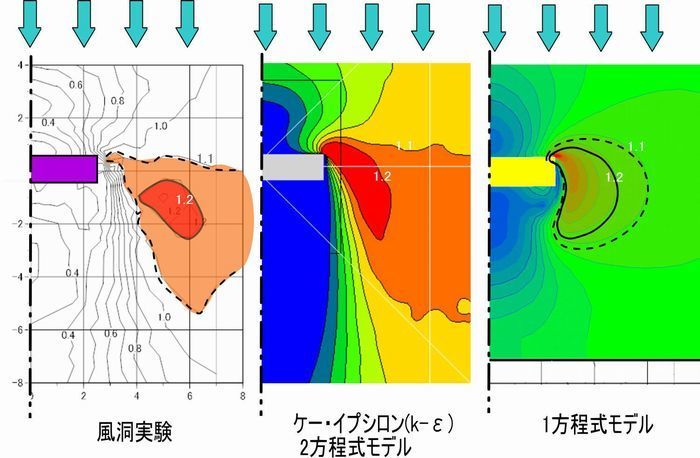
ケー・イプシロン(k-ε)2方程式モデルの結果は風洞実験に近い。しかし、1方程式モデルでは異なる。
風洞実験
風速比が1.1倍となる茶色の範囲は、建物の側方から風下側にかけて丸みを帯びた三角形に近い形状に分布しており、その右側の末端は建物の中心から8Lの範囲より、さらに外側まで広がっています。幅75メートルもの板状建物になりますと、正面に当たった風は側方に勢い良く吹き出す風の量が多くなるため、建物の角からかなり離れたところまで風速増加の影響を及ぼします。風速が1.2倍となる風速増加域(赤)は、1.1倍の範囲(茶色)に比べて大きさはかなり小さくなっており、その中心は建物の妻側の角から斜め後方のやや離れた位置にあります。
これは、ビル風の現象は、建物の前面で圧力エネルギーを蓄え、建物角から吹き出すときにその風を放出する、圧力から風速へのエネルギー変換と考えられます。圧力の最も高い場所は建物の風上側の中心の7割程度の高さにあるため、上空では地上より強いエネルギーとなり、その吹きおろしの風も伴って、建物からやや離れた場所に最高風速が発生するのです。
ケー・イプシロン(k-ε)2方程式モデル
風速が1.1倍となる風速増加域(茶色)は、風洞実験の場合とほぼ近いものとなっています。風速比が1.2倍となる範囲(赤)は、その中心はから建物の妻側角から斜め後方に伸びています。これらの風速増加域の形状から、ケー・イプシロン(k-ε)2方程式モデルでは、建物の正面の壁が受けたエネルギーを建物側方に勢い良く噴出す、風の慣性力をうまく表しているといえます。また、風のエネルギーがどこまで及ぶか、すなわち建物の近傍でビル風が発生して、その風がどの程度の距離で減衰するかについても正確に表しているといえます。
1方程式モデル
この方式では風速比が1.1倍となる風速増加域(点線)は、前述の2つの方式とは全く異なり、建物の妻側の角の近くに円形に近い形で存在しています。また、風速比が1.2倍となる範囲(実線)も、形状が1.1倍とほぼ同じで、同心円に近い形となっており、その範囲は前述の2つの方法に比べて最も大きくなっています。しかもその内側はさらにあり得ないくらい風速比が大きくなっており、最大の風速比は2.0程度にもなっています。1方程式モデルによる計算では建物の風下側の渦の減衰が遠くまで正しく計算できない一方、平均風速を風洞実験に近づけるため、便宜的に風速を高めに出さざるを得ず、結果的に建物のそばでにき急激に風速比が大きくなるよう、渦粘性の計算式を補正しているためと考えられます。
お気軽にご相談ください

お気軽にご相談ください
| 受付時間 | 9:00~17:00 |
|---|
| 定休日 | 土曜、日曜、祝祭日 |
|---|
マンション建設計画地の風害問題で住民紛争が発生してお困りの、マンションディベロッパー担当者様、建設会社の現場監督、設計部担当者様。ビル風対策・調査なら、コンサルティング経験豊富な不動産環境センターにお任せください。ビル風・暴風の原因調査・対策から風害予測調査、風洞実験、コンピューターシミュレーションまで対応しております。お気軽にご相談ください。
| 対応エリア | 東京都、神奈川県、埼玉県、千葉県、北海道、宮城県、愛知県、大阪府、岡山県、広島県、福岡県、熊本県 |
|---|
無料相談実施中
サービス案内
ビル風入門
気象データ
神奈川県
全国主要都市
調査実績
ビル風、風害に関する規制
会社紹介
お客さまサポート
株式会社
不動産環境センター
主な業務地域
東京都、神奈川県、埼玉県、千葉県、北海道、宮城県、愛知県、大阪府、岡山県、広島県、福岡県、熊本県

