〒103-0008 東京都中央区日本橋中洲2-3 サンヴェール日本橋水天宮605
受付時間 | 9:00~17:00 |
|---|
定休日 | 土曜、日曜、祝祭日 |
|---|
キャノピーモデルはこのようにして開発された
1980年ごろ建築分野においても高層建物の風害防止の観点から樹木まわりの風速分布、流体抵抗に関する研究がされていましたが、当時は見付面積を代表面積として抵抗係数を算定したもので、樹木の厚みが考慮されていない2次元的な扱いをしていました。しかしこれでは建物周りのビル風の検証に用いることが困難なので、 3次元的な奥行きのある樹木としのモデル化が必要でした。
このため、キャノピーモデルと呼ばれる、植物の葉を小さな平面の集合体と考えて、立体的空間の中に多数平面を用意して、風に対して抵抗を生み出すモデルが考案されました。この先駆的な研究は1996年ごろ、国立建築研究所の大橋様らによって、樹木模型を用いた風洞実験に基づいて、数値流体計算で予測※1することにより行われました。(研究の詳細は参考文献※1をご覧ください。建築学会図書館よりネットから論文コピーを入手することが可能です。)

上の図はこの実験に用いられたキャノピーモデルの実験樹木(模型)の写真です。この実験樹木に風を流すと、下の図のように実際の樹木と同じような風下側の風速低減効果が得られています。その後も樹木周辺の風環境についての研究が行われ、日本建築学会環境系論文集に「葉面積密度を代表面積とした樹木の抵抗係数に関する風洞実験」※2として報告されています。
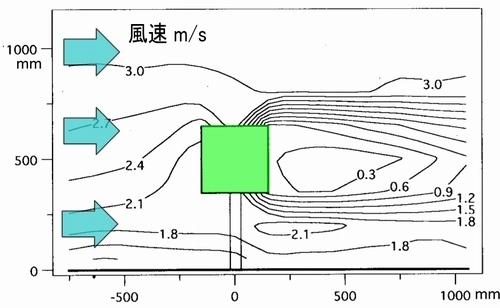
その後、2001年ごろに、加藤敦子, 持田, 吉野, 村上の4氏らによってk-ε2方程式モデルにキャノピーモデルを組み込む計算式が提案されました。これは、日本建築学会大会において「植生Canopyモデルを組み込んだk・εモデルによる単独樹木周辺の風速分布の予測」※3として報告されています。なおこの共同研究者の村上先生とは風環境評価尺度「村上法」を開発された先生(当時慶應義塾大学教授)です。
この計算式の考え方は、風が樹木に当たると枝葉によって風の乱れ(乱流エネルギーk)が生じ、そのエネルギーが渦となって散逸(散逸率ε)していくというモデルです。一般的な風の流れに対して、樹木が乱流エネルギーkと散逸率εをどれだけ増すか、実験をもとに数値流体計算によってそれらの値が確認されました。具体的には、風の流れの計算式、k-ε2方程式に、葉の抵抗係数(Cf)が加えられ、その抵抗係数は葉面積密度との積として与えられ、一方、樹木によって乱流エネルギーが消散していく分については消散率(Cpε)を定数で仮定され、風速の結果が風洞実験と一致するように定数を決めたのです。
参考文献
※1 大橋征幹:「41288 樹木模型周辺の気流分布に関する風洞実験」、日本建築学会大会学術講演梗概集、(近畿)1996年9月
※2 神山健二、大橋征幹、成田健一:「葉面積密度を代表面積とした樹木の抵抗係数に関する風洞実験」日本建築学会環境系論文集 第578号, 71-77, 2004年4月
※3 加藤敦子、持田灯、吉野博、村上周三:「40456 植生Canopyモデルを組み込んだk・εモデルによる単独樹木周辺の風速分布の予測」日本建築学会大会学術講演梗概集、(関東)2001年9月
お気軽にご相談ください

お気軽にご相談ください
| 受付時間 | 9:00~17:00 |
|---|
| 定休日 | 土曜、日曜、祝祭日 |
|---|
マンション建設計画地の風害問題で住民紛争が発生してお困りの、マンションディベロッパー担当者様、建設会社の現場監督、設計部担当者様。ビル風対策・調査なら、コンサルティング経験豊富な不動産環境センターにお任せください。ビル風・暴風の原因調査・対策から風害予測調査、風洞実験、コンピューターシミュレーションまで対応しております。お気軽にご相談ください。
| 対応エリア | 東京都、神奈川県、埼玉県、千葉県、北海道、宮城県、愛知県、大阪府、岡山県、広島県、福岡県、熊本県 |
|---|
無料相談実施中
サービス案内
ビル風入門
気象データ
神奈川県
全国主要都市
調査実績
ビル風、風害に関する規制
会社紹介
お客さまサポート
株式会社
不動産環境センター
主な業務地域
東京都、神奈川県、埼玉県、千葉県、北海道、宮城県、愛知県、大阪府、岡山県、広島県、福岡県、熊本県

