たばこや線香から立ち上る煙は、静かな室内では真上に向かってきれいな筋を作ります。ところが建物の外では風があるため、煙突などの煙は無数の渦を作り，拡散していきます。この落ち着いてまっすぐに流れる様相を層流 といい、一方乱れる複雑な流れを乱流 と呼び両者を区別するパラメータをレイノルズ数と呼んでいます。一般的に建物周辺の風のレイノルズ数は10000〜数10万ともいわれ、十分乱れの大きい乱流といえます。

　ビル風の流体計算では、平均的に乱流が生じている状態を取り扱いますが、こうした流れは、流体の運動方程式であるナビエ・ストークス方程式で表現できると考えられています。非圧縮性の前提で考えると，ナビエ・ストークス方程式は次式で表されます。

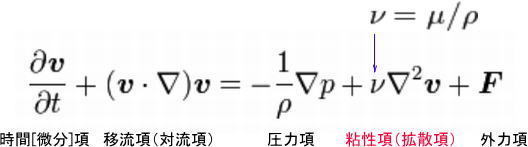
　ここでvは流体の流速で、密度をρ、圧力をp、単位質量当りの外力をF、粘性率をμ（一定）、としています。∂や∇などの記号はベクトル解析で出てくる記号で、偏微分、ナブラを表しています。この式の詳しい解説はウィキペディアなどをご参照願います。

　流体解析とは、この方程式の未知数、流体の速度(ベクトル)と圧力を解くことであり、そこで最も難解なことは粘性項を解くことです。なぜなら、流体の粘性は流速によって変化し、その値は非線形に変化するので、ふつうの方程式では解けないからです。

　この粘性項をどう正しくとらえるかで流れの性格が決まってきます。

　この粘性項(拡散項)を解く方法として、次の3つの方法が存在し、当社ではその最も信頼できるケー・イプシロン(k-ε)2方程式モデルを採用しています。

• 0方程式モデル(混合長モデル)
• 1方程式モデル
• ケー・イプシロン(k-ε)2方程式モデル

0方程式モデル

　粘性を定数として解く最もシンプルな方法であり、静止した空気と流れのある空気の間では一定の距離の範囲内で空気が混合して渦が生じるという考え方のモデルです。静止した空気とは早く言うと壁面とも例えられますので、壁面と流れの中心との関係だけであって、その風上からの風の影響は含まれていません。いわば、障害物を設けた箱の中に、粘性の非常に大きい葛湯みたいな液体を流し込んで押し出すような流れにたとえることができます。大まかな流れの向きは確認できますが、疑似的な流れの表現にすぎません。

　1方程式モデル

　やや進化した方法で、渦の大きさをとらえるのに、乱流エネルギーを用います。そして、乱流エネルギーが渦の流れとして、下流に流れて行って混合する様子を計算するというものですが、計算を単純化するため混合する長さを経験的に定数としています。

　0方程式モデルも1方程式モデルも、ともに計算量が少なく、10〜20年前のコンピューター計算が遅かった時期に用いられました。考え方としては流体の粘性を高めて大きな渦が発生しないようにして解く、感覚的にはシャンプー液やサラダオイル、葛湯などの流れにたとえることができます。大まかな流れの向きは確認できますが、これらの計算式では勢いよく吹き出した風がその先の物にぶつかる(慣性力)とか、建物の角から風が勢いよく吹き出す現象(剥離)に対して、一方その脇では逆流している(逆流)などの現象はよく確認できません。疑似的な流れの表現にすぎないため、精度が悪いので今ではお勧めできるものではありません。(ただし一部の調査機関では価格が安いことや、流体計算の精度に詳しくないという制約から採用してしまっている機関がありますのでご注意願います。)

ケー・イプシロン(k-ε)2方程式モデル

　数値流体力学に利用される乱流モデルのなかで，設計などの工学的利用に最もよく使われています。この考え方を簡単に説明すると、乱流によって発生する応力、すなわち止まっている流体と動いている流体の間に発生する力を、速度勾配(2点間で速度が変化する割合)に比例すると仮定しています。このときの、いわば摩擦係数に相当する比例係数を渦粘性係数と呼んでおり、k-εとはこうした乱れの運動エネルギー kとその散逸率εによって渦粘性を表現する計算式といえます。すなわち、建物に風が当たるとそのすぐ風下側には大きな渦が発生し、この渦が風下に流れていくにしたがって、小さな渦に分散して、やがて消散していくという現象です。現象的に理解しやすいモデルですし、大きな渦で発生するエネルギー(乱流エネルギー)と、そのエネルギーが渦によって消散する現象は実験でも確認されています。そして kとεの輸送方程式は、最初にご説明したナビエ・ストークスの運動方程式と連立して解かれます。

　以上のことから、流れの渦の粘性を解くのに、乱流エネルギーとエネルギーの消散率を連立させて解く、k-ε2方程式モデルが、今日最も信頼性の高いモデルとして使用されており、その方式を採用した当社のビル風予測解析業務は、ビル風予測という実用上の計算において十分信頼性を置いてもらえるものと自負しております。

　ケー・イプシロン(k-ε)2方程式モデルの解析結果は、他の方式と比べて相当計算結果が違います。まず、1方程式モデルと比較してみましょう。下の図は高さ45メートル、幅75メートル、奥行き15メートルの板状のマンションのモデルです。高さは15階建て相当です。この建物に正面から風が吹いてきた場合に、建物側方にできる風速増加域を計算してみました。風速増加域とは、建物の建設前後で比べて、風速の比が1．1以上となる範囲のことで、いわゆるビル風の範囲を表しています。

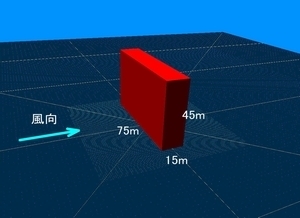
　下の図は、上の図に表す建物の風速増加域を、①風洞実験、②ケー・イプシロン(k-ε)2方程式モデル、③1方程式モデルでそれぞれ求めたものです。いずれも当社が行ったものであり、平面的な風速の分布を(左右対称なので)建物の右側部分だけ表して比較しています。

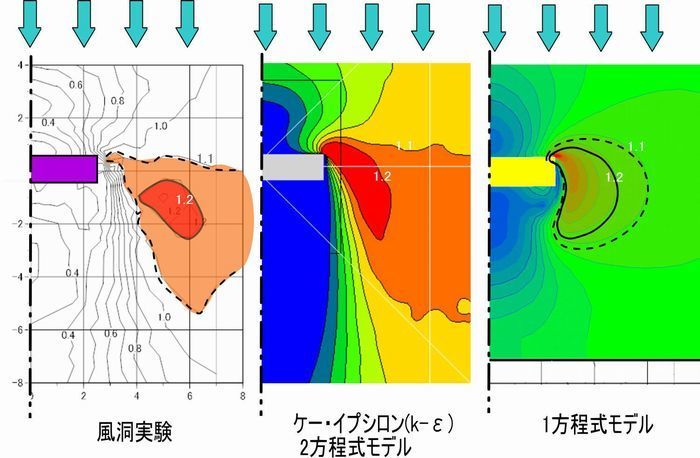
ケー・イプシロン(k-ε)2方程式モデルの結果は風洞実験に近い。しかし、1方程式モデルでは異なる。

　風洞実験

　風速比が1.1倍となる茶色の範囲は、建物の側方から風下側にかけて丸みを帯びた三角形に近い形状に分布しており、その右側の末端は建物の中心から8Lの範囲より、さらに外側まで広がっています。幅75メートルもの板状建物になりますと、正面に当たった風は側方に勢い良く吹き出す風の量が多くなるため、建物の角からかなり離れたところまで風速増加の影響を及ぼします。風速が1.2倍となる風速増加域(赤)は、1.1倍の範囲(茶色)に比べて大きさはかなり小さくなっており、その中心は建物の妻側の角から斜め後方のやや離れた位置にあります。

　これは、ビル風の現象は、建物の前面で圧力エネルギーを蓄え、建物角から吹き出すときにその風を放出する、圧力から風速へのエネルギー変換と考えられます。圧力の最も高い場所は建物の風上側の中心の7割程度の高さにあるため、上空では地上より強いエネルギーとなり、その吹きおろしの風も伴って、建物からやや離れた場所に最高風速が発生するのです。

　ケー・イプシロン(k-ε)2方程式モデル

　風速が1.1倍となる風速増加域(茶色)は、風洞実験の場合とほぼ近いものとなっています。風速比が1.2倍となる範囲(赤)は、その中心はから建物の妻側角から斜め後方に伸びています。これらの風速増加域の形状から、ケー・イプシロン(k-ε)2方程式モデルでは、建物の正面の壁が受けたエネルギーを建物側方に勢い良く噴出す、風の慣性力をうまく表しているといえます。また、風のエネルギーがどこまで及ぶか、すなわち建物の近傍でビル風が発生して、その風がどの程度の距離で減衰するかについても正確に表しているといえます。

　1方程式モデル

　この方式では風速比が1.1倍となる風速増加域(点線)は、前述の2つの方式とは全く異なり、建物の妻側の角の近くに円形に近い形で存在しています。また、風速比が1.2倍となる範囲(実線)も、形状が1.1倍とほぼ同じで、同心円に近い形となっており、その範囲は前述の2つの方法に比べて最も大きくなっています。しかもその内側はさらにあり得ないくらい風速比が大きくなっており、最大の風速比は2.0程度にもなっています。1方程式モデルによる計算では建物の風下側の渦の減衰が遠くまで正しく計算できない一方、平均風速を風洞実験に近づけるため、便宜的に風速を高めに出さざるを得ず、結果的に建物のそばでにき急激に風速比が大きくなるよう、渦粘性の計算式を補正しているためと考えられます。

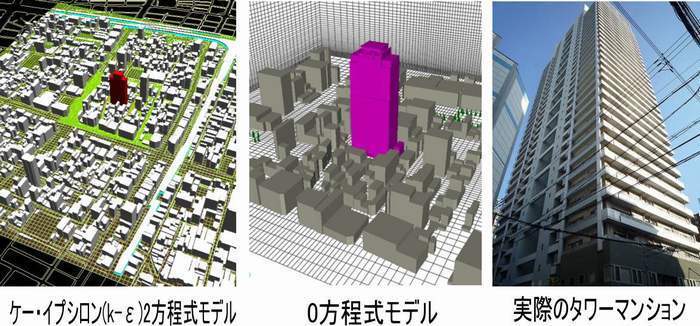
　ケー・イプシロン(k-ε)2方程式モデルを実際のタワーマンションのビル風の予測に使用するとどうなるかを比較検証してみました。0方程式モデルとこんなに違うということがわかるかと思います。

　比較検証するモデルとなったタワーマンションは、大阪市内にある35階建てのマンションです。計算のモデルと建物の外観を以下に示します。左から順に、ケー・イプシロン(k-ε)2方程式モデル、0方程式モデルの計算領域、実際のマンションの写真の順です。

計算結果

風向: 西南西

　ケー・イプシロン(k-ε)2方程式モデルによる予測結果

　大阪で最も頻度の高い西南西の風における風速分布の結果です。ケー・イプシロン(k-ε)2方程式モデルでは、この程度の大きさの計算領域ですと、ワークステーションクラスのコンピュータで1日程度の計算時間が必要です。

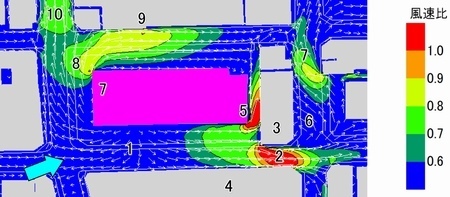
　k-ε2方程式モデルの結果では、まず建物の正面に風がぶつかり、1で吹き下ろし、ここから左右に分かれて吹いていきます。その1つは建物の右下の2で風速比が最大1.0となっています。この場所が東隣の建物3と向かいの建物4で作られるビルの谷間に相当することから、風の流路がオリフィスのように絞られて風速が高まっている様子が伺えます。こうした、流路が狭まると圧力が増して流速が高まる現象は、流体の原理ベルヌーイの法則に従っており納得しやすいものです。

　さらに南東側の建物の角5を過ぎた風は、隣のビル3との間で、やはりオリフィスとなるため、風速比1.0となっています。そしてその右の方には、建物から吹き下ろした風が左回りの渦となって6で逆流を作っており、その結果7の、こちらもビルのオリフィスとなるため風速比0.9となっています。

　一方、1から北側に分かれた風は北西側の角7で風速比0．9となりますが、すぐに建物から剥離して、向かいの建物9にぶつかって風速比0．9となります。前述の風洞実験の結果と同じで、角を通過した風は壁から剥離してやや離れた地点で最高風速を示すという、流体の慣性力を考慮すると納得しやすい結果となっています。このほか8を北方向に交差点を直進して通過した風は、10でやはりビル間のオリフィスとなるため風速比0.7となっています。

　0方程式モデルによる予測結果

　この方式では粘性の係数を流速によらず(大きめの)一定値と仮定して簡略に検査を行います。この程度の大きさの計算領域ですと、ふつうのノートパソコンで数分で計算可能です。

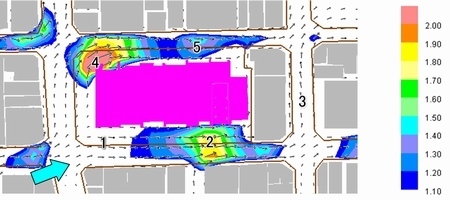
　風の流れは、まず1で風が建物にぶつかりますが、吹き下ろしの風もなく、不思議ときれいに2方向に分かれています。右方向に進んだ風は、建物の3分の2程度進んだところで2の最高風速を示し、そこを通過すると、オリフィスに差し掛かったにもかかわらずここで減速します。2の風速比は1.8程度と大きな値となっています。そしてさらにその下流側の3周辺では、逆流もなく、風速も大きくなってはいません。実際の建物では風下側のビルの裏側3のような場所では、高層建物からの吹きおろしの風があり、風速比が本来高まるはずの場所ですが、この計算では納得しにくい結果となっています。

　そして、1から北方向に別れた風は、4の角で最高風速、なんと風速比2.0とあり得ない値となっています。そして建物の角を吹きすぎると急激に減速し、その後再び建物の3分の2程進んだところ5で風速比1.4を示し、減速して行きます。このように0方程式の計算結果では、風が上流からどのように流れてくるかといった状況はあまり関係がなく、建物との位置関係でほとんど風速が決まってしまって、現実の風の流れとはやや違った傾向を示しています。そして、k-ε2方程式モデルに比べてかなり大きい風速比となっているといえます。

風向: 北東

　ケー・イプシロン(k-ε)2方程式モデルによる予測結果

　さらに風向を加えて、反対の北東、すなわち冬の卓越風についても検証してみましょう。まずk-ε2方程式モデルからです。

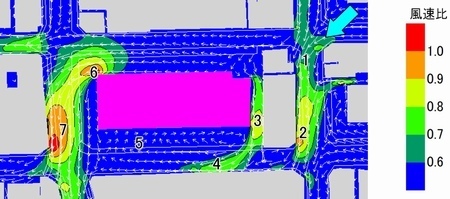
　風の流れは、1で建物にぶつかりますが、ここでは風速はあまり大きくはならず、この風下の2で風速比0．9となります。また建物の直近では、吹き下ろし風がビルのオリフィス3で風速を増し、その後慣性力があるために吹き出して、向かいのビル4に吹き付けます。k-ε2方程式モデルでは、こうした流路が狭まると風速が大きくなるという自然な現象が表現できています。そして、最も風下側5に行くと、逆流域となって上空とは逆方向の風となっており、これも実際のビル風で観測できる現象です。

　一方、1から西方向に別れた風は、6の角で最高風速、風速比1.0となっています。そして建物の角をすぎるといったん減速しますが、その後向かい側のビルの角7に吹き付けて、再び風速比1.0に増速しています。このように建物の角から剥離した数は、4や7といった建物からやや離れた場所で風速を高めます。しかし、そこは計画地内では無いため、植栽等の対策ができず対策困難なビル風問題となっています。k-ε2方程式モデルはこのような問題を見落とすことなく、安全側の評価でビル風の危険性を示してくれることから、信頼できる計算手法といえます。他方、0方程式モデルではこの問題を見過ごす危険性があり、中高層建物ビル風の評価にはふさわしくないと考えられます。

　0方程式による予測結果

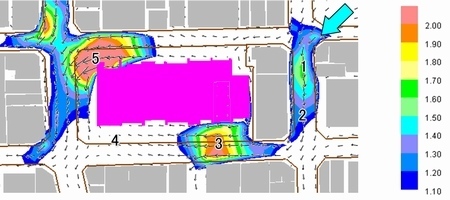
　最初に風上側の建物に風がぶつかったところ1で風速比が高まり、すぐに減速します。前述のk-ε2方程式モデルで見られたような下流側の2で風速が高まる現象は表現できていません。さらにその風下3では風速比は、オリフィスを過ぎたところでなんと2.0を示し、すぐに減速しています。風に慣性力があるわけではなく、建物との位置関係によって風速が決まっているようです。そして建物の風下側4では、逆流や吹き下ろしの風もなく、ほぼ1方向に風は流れています。

　一方、1より西方向に別れた風は、5の角で最高風速、風速比2.0となっています。そして建物の角を吹きすぎるとやはり減速し、その後は向かいビルに吹き付けることもなく減速しています。このように0方程式モデルの計算では建物の角付近で必ず風速が高まり、建物の近傍の剥離風の検討には有効です。しかし、風が勢い良く吹き抜ける慣性力を表せないため、建物からやや離れた場所での強風域を見落とす危険性があり、中高層建物ビル風の評価にはふさわしくないと考えられます。

　この0方程式モデルの予測計算プログラムは、建築設計者が設計時の建物のビル風を改善するための設計ツールとして作られたものであり、計算精度よりも使い勝手の簡便性に重きが置かれています。逆にビル風問題の検証用の手法としては、前述のような対策困難な近隣のビル風問題を見落とす危険性があるり、本来は使うべきではないと考えられます。

　当社が用いるビル風用解析プログラムは株式会社大林組の技術研究所で開発され、その開発者らによって、風洞実験とのベンチマークテストが行われています。さらにその後、日本建築学会、風環境数値計算ワーキンググループによっても詳細に検証され、その結果は、「市街地風環境予測のための流体数値解析ガイドブック」にまとめられています。これらの結果についてご紹介します。これらをご覧いただくことによって、当社のビル風解析の信頼性をご理解いただけるものと考えます。

　大林組技術研究所による検証結果

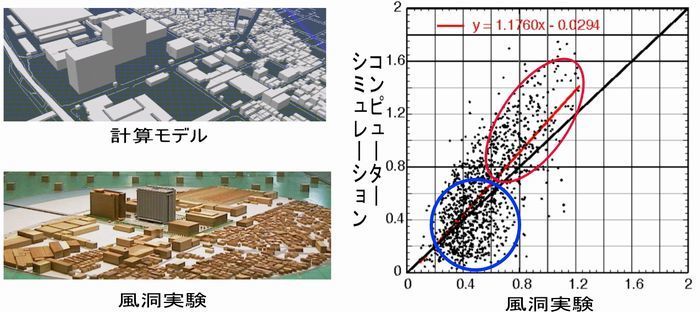
　大林組技術研究所はビル風解析プログラムZephyrus(ゼフィルス)を開発され、風洞実験とのベンチマークテストもされていらっしゃいます。当社はそのプログラムを採用しており、その結果について同社技術研究所報から抜粋してご説明します。解析をしたエリアは河川に沿った低層住宅が立ち並ぶ地域に隣接して、工場建物が建設された地域でした。計算モデルと風洞実験の模型を下の写真に示します。

　下左の図はその計算結果で、下右図は風洞実験とコンピューターシュミレーション結果の値を散布図に表したものです。この図からわかるように、コンピュータ・シュミレーションは風洞実験と相関があり、赤丸で示す強風域ではy=1.17xのグラフ近く、特に相関性が高いといえます。一方、青丸で示す低風速域ではやや相関性が低下しますが、ただし弱風域に相当するため、ビル風解析の主要な対象エリアではないということです。ビル風解析では、強風現象が対象となりますので、弱風域での相関性はそれほど問題とはならないのです。

　日本建築学会、風環境数値計算ワーキンググループによって検証された結果についてご説明します。同ワーキンググループでは風の数値解析(コンピュータ・シミュレーション)の信頼性を高めるため、現在開発されている数々の手法について検証し、その精度について「市街地風環境予測のための流体数値解析ガイドブック」にまとめています。当社が用いるビル風用解析プログラムはzephrus(ゼフィルス)という大林組によって開発されたプログラムであって、大林組技術研究所の研究者が多数、前述のワーキンググループに参加されて、風洞実験とのベンチマークテストを行われました。

　このベンチマークテスト(風洞実験と計算の比較)では、下の図のような新潟市内の高さ60mのビルと18mのビル2棟について、市街地模型を用いて風環境評価が行われています。左の図は風洞実験の模型で水色の用地が建設前の様子です。右はコンピュータ・シミュレーションのモデルであり、黄色の計画建物が建設されています。

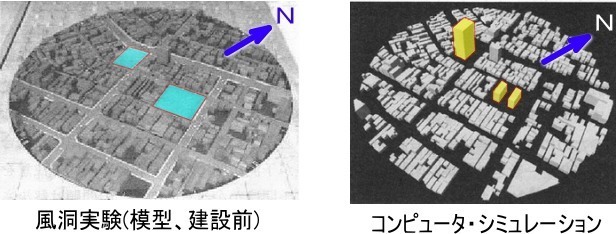
　この模型、モデルに対して建設地の新潟地域の卓越風向である北北東と西の2風向について、比較実験されています。

　検証結果

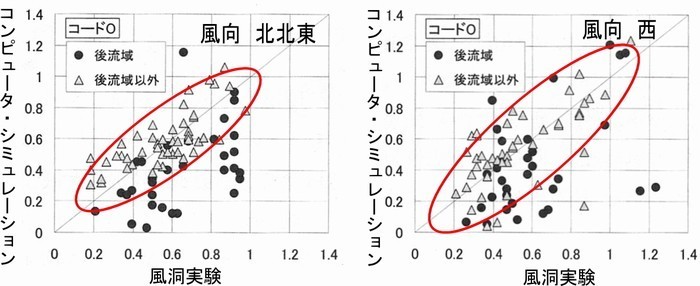
　建物の後流以外、すなわち建物の側方や斜め後ろのビル風の影響を直接受ける、比較的風速の大きい場所(△のプロット)は赤い楕円で示す範囲内に入っており、コンピュータ・シミュレーションの結果は風洞実験と高い相関を示しています。北北東、西風ともにこうした傾向はほぼ共通しています。このことから、風速の大きい、ビル風の危険性の高い場所ではコンピュータ・シミュレーションは精度よく計算できているということです。

　なお、グラフには●でプロットされた建物の後流のデータも示されています。これらは概ねy=xの線より下にあり、コンピュータ・シミュレーションの結果は風洞実験より小さめの値となっています。これはコンピュータ・シミュレーションでは平均流を計算するため、建物風下側のカルマン渦等を表現できず値が小さくなりがちだからです。カルマン渦とはビル風が建物に当たって通過した後、風下側に作る左右交互に発生する渦のことを言います。風洞実験ではカルマン渦が発生するかまたは、建物の後流側は風の乱れが大きく、風速センサーのサーミスター風速計では細かい風速まで計測してしまうので、値が大きくなってしまうということです。ただし、ほとんどが弱風域に相当しますので、風環境評価ではあまり問題になりません。

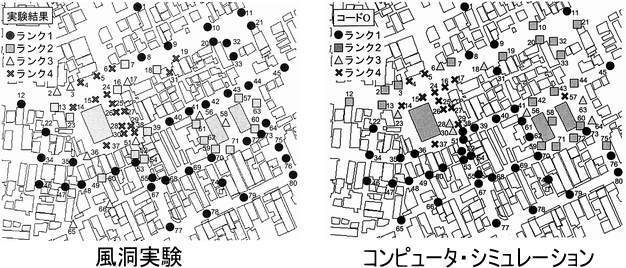
　村上法による風環境評価

　ベンチマークテストは、さらに村上法による風環境評価も行っており、その評価結果は下の図のように良く一致しています。建築学会ワーキンググループではこの結果に対して次のように知見をまとめています。。

• 高層建物近傍の風速増加領域においては、計算と実験は全体的に良い相関を示した。
• 村上らの風環境評価尺度のランク評価で風洞実験結果と比較した場合も、両者は一部では差があるものの、全体的にはよく一致した。