風洞気流の調整方法
(1)運動学的相似
風洞気流に関しては,実際の気流条件とできる限り相似側を一致させることが望ましく、以下の指標を考慮します。
・平均風速の鉛直分布
・境界層高さ
・粗度長
・乱れのスケール
・乱れの強さ
ただし、測定の目的が平均風速の場合は,平均風速の鉛直分布と境界層高さあるいは粗度長を考慮すれば有効なデータを得ることができます。しかも平均風速の鉛直分布を指数則に基づいて再現すれば,粗度長についての配慮はそれほど必要としません。乱れのスケールや乱れの強さの相似則は変動風速や最大瞬間風速等を測定目的とした場合のものだと考えればよく、一般的な風環境評価では平均風速の測定となるためそれほど影響はないと考えてよいでしょう。
境界層高さなど高さ方向の模型化範囲は,超高層建築物等の場合は建築物高さの1.5倍以上,比較的低層の市街地に関しては市街地の建築物高さの2〜4倍程度までの、いずれか高い方とします。
(2)実験風速の決定
測定機器の分解能や誤差の大きさを考慮して平均風速5〜15m/sの範囲で実験は行います。一方、レイノルズ数は,実現象と一致させることは事実上困難であり、建築物の形状が角張っている場合は建築物周辺の流れの状態に大きな差異がないことから,レイノルズ数が一致しなくても有効なデータを得ることができると考えてよいでしょう。
(3)境界層(鉛直方向の風速分布)の作成
境界層風洞では、上空にいくほど風速が大きくなり、一定以上の上空は風速も一定になるという自然の風を作り出します。境界層風洞では、鉛直方向の平均風速分布が自然の風と相似させるため、風洞入口にスパイヤーという槍状の障害物を置いたり、床面にラフネスブロックと呼ぶサイコロ状の突起物を設置して、空気の乱れを発生させて、地上付近の風を作り出します。
下の写真は、風洞の下流側の出口から、風の流れの上流に向かって、気流とは逆向きに内部を見通した写真です。手前の白い風洞模型の奥に床面にたくさんの突起物が設置されており、このラフネスブロックは地上付近の建物を模擬して、細かい乱れを発生させています。模型の最も近くには木製の矩形建物を模擬したブロックが等間隔で並べられており、その向こう側には金属製の円筒形のブロックが並んでいます。こうしたブロックは高さを調節することで地表面の抵抗を変えて、後述する田園の地帯の風や市街地の風を作り出します。また一方、風洞の奥には水色の縦の槍状の障害物が縦に大小各5、6本並べられています。これがスパイヤーと呼ばれる空気抵抗器であり、こちらは地上付近から上空までの風速分布と乱れを発生させます。

自然の風は、鉛直方向の平均風速分布は、風速の比が高さの比のべき乗に比例するという、べき法則あるいは、対数法則に従うことが観測結果や理論から明らかとなっています。
下図は、地表面粗度区分Ⅱ(田園地帯)の地上10mでの平均風速V₀を基準として表示した場合の高さ方向の風速分布です。すなわち風速と高さの関係は下図に示すように、上空ではどのような地域でもほぼ同じ風速を示しています。しかし、高さが低くなると、市街地では高層建物の凹凸形状などの抵抗によって、地上に近付くにつれて風速が大きく減衰します。一方、海上では海面の凹凸がほとんど無いため風速の減衰は小さいのものとなっており、海面付近まで強い風が保たれます。こうした地域によって異なる境界層の鉛直方向の風速分布を風洞実験で作り出すため、前述のスパイヤーとラフネスブロックを駆使して風を調整しています。
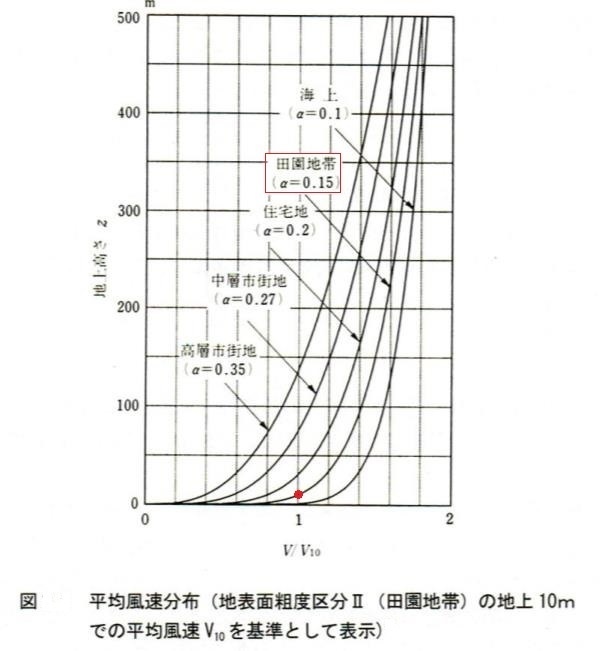
この鉛直方向の風のべき法則、風速Vと高さZの関係分布は下記の式のように表すことができ、このαをべき指数と呼んでいます。αは地表面粗度区分(地表面の凹凸の状態)に応じて決まり、住宅地では0.2、中層市街地では0.27程度となっています。
Vz₁/Vz₂ = (Z₁/Z₂)α
| 地表面粗度区分 | |||||
| I | Ⅱ | Ⅲ 住宅地 | Ⅳ 中層市街地 | V 高層市街地 | |
| 平均風速分布べき指数α | 0.10 | 0.15 | 0.20 | 0.27 | 0.35 |


